Pearson correlation coefficient interpretation/How calculated
Knowledge circulates from the general to the particular, in this sense the explanation of new phenomena can be studied by the relationship it has with events of the same phenomenon, which is what is frequently done in the field of research. Due to the foregoing, there is a need to establish the relationship between two quantitative variables in a group of study subjects. Pearson correlation coefficient interpretation
The science of statistics has methods that make it possible to measure this relationship, with the following objectives:
- Determine if both variables are correlated, that is, if for lower or higher values of one variable, the values of the other variable tend to be equally lower or higher.
- Predict the value of a variable, taking a certain value from the other variable.
- Estimate the level of correspondence between the values of both variables.
What is Pearson’s correlation coefficient?
Pearson’s Correlation Coefficient is a measure of the correspondence or linear relationship between two random quantitative variables. In simpler words, it can be defined as an index used to measure the degree of relationship between two variables, both quantitative.
Having two variables, the correlation facilitates estimates of the value of one of them, with knowledge of the value of the other variable. Pearson correlation coefficient interpretation
This coefficient is a measure that indicates the relative situation of the events with respect to the two variables, that is, it represents the numerical expression that indicates the degree of correspondence or relationship that exists between the 2 variables. These numbers vary between limits of +1 and -1.
How is it calculated?
To have a guide that allows:
- Establish the contiguous variation of the two variables
- Compare the different cases with each other
To do this, the Pearson correlation coefficient is used, defined as the covariance that occurs between two standardized variables and is calculated with the following expression:
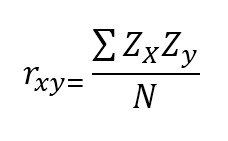
How does that interpret Pearson’s correlation coefficient?
Its dimension indicates the level of association between the variables. Pearson correlation coefficient interpretation
- When it is less than zero (r <0) It is said that there is a negative correlation: The variables are correlated in an inverse sense.
High values in one of the variables usually correspond to low values in the other variable and vice versa. The closer the value is to -1 said correlation coefficient, the more evident the extreme covariation will be.
If r = -1 we speak of a perfect negative correlation, which supposes an absolute determination between both variables, in a direct sense a perfect linear relationship of negative slope coexists.
- When it is greater than zero (r> 0) It is said that there is a positive correlation: Both variables are correlated in a direct sense.
High values in one of the variables correspond to high values in the other variable, and in an inverse situation the same occurs with low values. The closer to +1 the correlation coefficient is, the more evident the covariation will be. Pearson correlation coefficient interpretation
If r = 1 We speak of a perfect positive correlation, which supposes an absolute determination between the variables, in a direct sense a perfect linear relationship with a positive slope coexists).
- When it is equal to zero (r = 0) The variables are said to be incorrectly related, it is not possible to establish some sense of covariation.
There is no linear relationship, but this does not necessarily imply that the variables are independent, as there may be non-linear relationships between the variables.
When the two variables are independent they are said to be uncorrelated, although the reciprocity result is not necessarily true. Pearson correlation coefficient interpretation
To conclude, it can be said that it looks more difficult than it turns out, especially if you have advanced technology, since today there are multiple programs that facilitate this task of calculating and interpreting the Pearson coefficient.



