The coefficient of determination , also known as r2 , is a term used in statistics, whose main function is to predict the result of hypotheses. This is essential in any study with scientific foundations and its applications can have a wide range, such as in economics, the study of markets or to determine the success of a product. How to calculate coefficient of determination?
There are several definitions about this well-known tool, which do not all coincide, so it is important to know each of them, such as those that are related to linear regression.
Definition of coefficient of determination
It is the correlation square that measures which part is explained in a certain variant as part of a variance, this means which one can be predicted through the variance of the other.
How is the coefficient of determination calculated?
Statistical models are intended to test or explain some random variable, this is done through other random variables that are known as factors. Since a variable considered random can be predicted through its measure and that for this case the variance will be the same mean square error, the maximum mean square error that can be accepted is the variance. How to calculate coefficient of determination?
The result can vary between 0 and 1 , this means that the closer it is to one, it will be more adjusted to the variable you are trying to test, while in the opposite case, that is, the closer it is to 0, the less reliable it will be since it will be less adjusted the model.
How is the coefficient of determination expressed?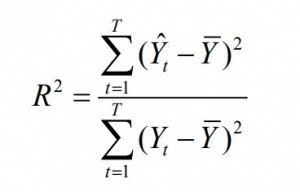
Here you can see a fraction in which the numerator is expressed as follows:
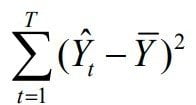Here it can be seen that in the variance expression the Y is circumflexed, which means that it is the estimate of a model, this is not the real value of Y but an estimate. Another difference with respect to this expression of the variance is that it is not divided by T since the denominator would also express it, then both are eliminated so that the expression is simplified in this way. How to calculate coefficient of determination?
Regarding the denominator, we observe that the only difference with the variance that can be noticed is that it is not divided by T or N
Applications of the coefficient of determination
There are many utilities that this formula has, for example, in the case of trying the number of points that a soccer or basketball player scores with respect to the number of games he plays, based on the assumption that the more games, the more points they will be. annotated. Let’s take into account 8 games.
The graph would show a sloping line, with a positive relationship, since as expected the more games played, the more points were scored, this graph would show a result above zero, which, as we mentioned before, would prove that it is adjusted to the real variable. How to calculate coefficient of determination?
Why does the fitted R squared arise?
What happens with R squared and the reason why the adjusted R squared is given has to do with the fact that inclusion does not penalize with respect to non-significant explanatory variables, this means that, if it is added to the model, for example 5 explanatory variables that do not have much relation with the score that this certain player has written down, the R squared will be higher or will increase.
R squared fitted
It is a measure that establishes the percentage explained by the regression variance with respect to the variance of the explained variable. You can see that it is the same as with R squared, however with the small difference that it penalizes the inclusion of variables. How to calculate coefficient of determination?
The R squared always increases even though the variables included in the mentioned model are not really relevant. To solve this problem it is applied that:
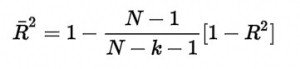
In this equation, N is referred to as the sample size and K corresponds to the explanatory variables. From the point of view of mathematical deduction at values above k, the adjusted R-squared will be further from the common R-squared.
Other functions of the coefficient of determination
Not only is it useful to explain or rather, to measure the explanatory capacity of a model, but at the same time it allows choosing which among several models is the most appropriate. This means that the models have the same dependent variables and the same number with respect to the variables that are known as explanatory, the most appropriate will be the one with a higher coefficient of determination. How to calculate coefficient of determination?
Clearly this may vary depending on the chosen model since it will not be the same in the case of a nested model, for example. The most important thing regarding this coefficient is its ability to predict the effectiveness of the proposed models or theories, this can be applied not only to numbers, this is vital to know if the predictions are good or bad.
