Stoichiometry

Stoichiometry is the way to calculate the amounts of reactants and products involved in a chemical reaction.

It comprises simple mathematical calculations to know the correct proportion of substances to be used.

The principles of stoichiometry are based on Ponderal Laws, related to the masses of chemical elements within chemical reactions. They include:

• Lavoisier’s Law : Also called the “Law of Conservation of Mass”. It is based on the following principle: ” The sum of the masses of the reacting substances in a closed container is equal to the sum of the masses of the products of the reaction “.
• Proust’s Law : Also called the “Law of Constant Proportions”. It is based on “ A certain compound substance is formed by simpler substances, united always in the same mass proportion ”.

Thus, atoms are not created or destroyed in a chemical reaction. Therefore, the number of atoms of a certain chemical element must be the same in the reactants and in the products.

How to make stoichiometric calculations?

There are several ways to solve problems with stoichiometric calculations . Let’s follow some steps for its resolution:

• Step 1 : Write the chemical equation with the substances involved;
• Step 2 : Balance the chemical equation . For this, it is necessary to adjust the coefficients so that reactants and products contain the same amount of atoms, according to Ponderal Laws ( Proust’s Law and Lavoisier’s Law );
• Step 3 : Write the values ​​of the substances, following the data of the problem and identifying what is asked;
• Step 4 : Establish the existing relationship between the number of moles, mass, volume. According to the following values:

• Step 5 : Make a simple rule of three to calculate the values ​​that are asked in the question or problem.

Example of Stoichiometry

1. How many moles of hydrogen gas are needed to form ammonia (NH ₃ ), knowing that the amount of nitrogen gas is 4 moles?

Step 1 : N ₂ + H ₂ = NH ₃

Step 2 : in the equation the amounts of atoms are not balanced. There are 2 nitrogen atoms and 2 hydrogen atoms in the reactants, while the product has 1 N and 3 hydrogen atoms.

Starting with nitrogen, we set the coefficient on the product: N ₂ + H ₂ = 2 NH ₃

The nitrogen was balanced on both sides, but the hydrogen was not.

N ₂ + 3 H ₂ = 2NH ₃ . Now yes!

Step 3 : Value given by the exercise: 4 moles of N ₂

Value requested by the exercise: how many moles of H ₂ ? We write: x moles of H ₂

Step 4 : Establish corresponding relationships when necessary. In this example there is no need, because it is mol to mol.

In the balanced reaction above, it is observed that the ratio is 1 mole of N ₂ reacting with 3 moles of H ₂ .

Step 5 : Make the rule of three.

Attention! Always put the values ​​of a substance over itself when setting up the rule of three, that is, in the example, nitrogen over nitrogen and hydrogen over hydrogen, as seen below:

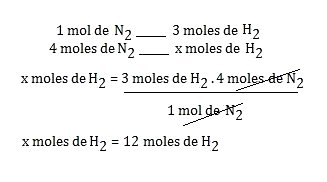
Solved Exercises of Stoichiometry

Exercise 1 (Mole with Mass)

1. How many grams of hydrogen react with 5 moles of oxygen to form water?

Resolution

1) H ₂ + O ₂ = H ₂ O

2) First balance the oxygen coefficient in the product ⇒ H ₂ + O ₂ = 2 H ₂ O.

And finally, balance the hydrogen 2 H ₂ + O ₂ = 2 H ₂ O

3) Problem data: x grams of H ₂ and 5 moles of O ₂

4) Mole to mass ratio: 1 mol of H ₂ corresponds to 2 grams of H ₂ (Molar Mass).

By the balanced equation: 2 moles of H ₂ react with 1 mole of O ₂ . Therefore, following the above relationship, 2 moles of H ₂ corresponds to 4 grams

5) Rule of three: 4 g of H ₂ _______ 1 mol of O ₂

x grams of H ₂ _______ 5 moles of O ₂

xg of H ₂ = 5 moles of O ₂ . 4 g of H ₂ / 1 mol of O ₂

x = 20

Then 20 grams of hydrogen react with 5 moles of oxygen to form water.

Exercise 2 (Mole with Volume)

2. What volume of oxygen, in liters, is needed to form 1 mole of liquid water (according to CNTP)?

Resolution:

1) H ₂ + O ₂ = H ₂ O

2) As seen above the balanced equation is: 2 H ₂ + O ₂ = 2 H ₂ O

3) Problem data: x liters of O ₂ and 1 mol of H ₂ O

4) Mole to volume ratio: 1 mol of O ₂ corresponds to 22.4L and 1 mol of H ₂ O corresponds to 22.4L

_{According to the equation, 1 mole of O 2} is needed to form 2 moles of H ₂ O. As the exercise asks for 1 mole of water, half of this proportion will be needed, that is, 1/2 mol of O ₂ to 1 mole of water.

5) Assemble the rule of three: 1 mol of H ₂ O _______ 1/2 mol of O ₂

22.4L of H ₂ O _______ x liters of O ₂

x liters of O ₂ = 22.4L of H ₂ O . 1/2 mole of O ₂ / 1 mole of H ₂ O

x = 11.2

It takes 11.2 liters of oxygen to form 1 mol of liquid water.